İrrasyonel sayılar

$\sqrt{2}$ sayısı irrasyoneldir

İrrasyonel sayılar, rasyonel sayılar kümesine dahil olmayan gerçek sayılardır. Payı ve paydası birer tam sayı olan bir kesir olarak ifade edilemeyen bu sayılara $\pi$ (pi sayısı), $e$ (e sabiti), $\sqrt{2}$ (2'nin karekökü) ve $\sqrt{3}$ (3'ün karekökü) örnek verilebilir. ${\mathbb{Q}}^{\prime }$ veya $𝕀$ ile gösterilir. Bu sayıların ondalık açılımı, kendini tekrar etmeden, sonsuza kadar sürer. Bu açılım irrasyonel sayıların hemen hemen hepsinde (örneğin pi sayısında, $\pi =3,141592653589\dots$) düzensizdir; ancak bir düzen de gösterebilir, örneğin bütün sayıların sırayla yazılmasıyla edilecek 0,12345678910111213... sayısı irrasyoneldir. İrrasyonel sayıların ilk gerçek değerini Archimedes kullanmıştır.

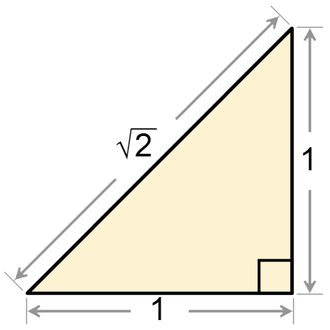
Bir dik üçgenin dik kenarları aynı uzunluktaysa ve rasyonel sayı ile ifade edilebiliyorsa, hipotenüs her zaman irrasyoneldir. Dik kenar $\chi$ ise, hipotenüs $\chi \sqrt{2}$ olacaktır.

Örnekler

Matematik sabiti pi sayısı (π), popüler kültürde sıkça rastlanan bir irrasyonel sayıdır.

• $5^{}\sqrt{(9/8)}$ irrasyonel sayıdır

• $\sqrt{2}$ irrasyonel sayıdır

• $\sqrt{3}$ irrasyonel sayıdır

• $3^{}\sqrt{7}$ irrasyonel sayıdır

• $3^{}\sqrt{6}4$ irrasyonel sayı değildir çünkü rasyonel karşılığı vardır $3^{}\sqrt{6}4=4$

• $\sqrt{(4/9)}$ irrasyonel sayı değildir çünkü rasyonel karşılığı vardır $\sqrt{(4/9)}=\frac{2}{3}$

Ayrıca bakınız

• Karekök 3

Sayı sistemleri Karmaşık $:ℂ$ Reel $:ℝ$ Rasyonel $:\mathbb{Q}$ Tam sayı $:\mathbb{Z}$ Doğal $:\mathbb{N}$ Sıfır: 0 Bir: 1 Asal sayılar Bileşik sayılar Negatif tam sayılar Kesir Sonlu ondalık sayı İkili (sonlu ikili) Devirli ondalık sayı İrrasyonel Cebirsel irrasyonel Aşkın Sanal