Dosya:Ehrenfest-paradox-disk.svg
Gezinti kısmına atla
Arama kısmına atla
Bu SVG dosyasının PNG önizlemesinin boyutu: 220 × 180 piksel. Diğer çözünürlükler: 293 × 240 piksel | 587 × 480 piksel | 939 × 768 piksel | 1.252 × 1.024 piksel | 2.503 × 2.048 piksel.
Orijinal dosya (SVG dosyası, sözde 220 × 180 piksel, dosya boyutu: 4 KB)
Özet
| Açıklama |
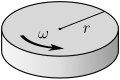
English: The Ehrenfest paradox in special relativity describes a spinning cylinder, which should contract around the circumference due to Lorentz-contraction, while its radius remains constant. The graphic shows rulers which rest in the laboratory system and rulers attached to the cylinder, which get contracted relatively to the laboratory system.
Deutsch: Das Ehrenfestsche Paradoxon der Speziellen Relativitätstheorie beschreibt einen rotierenden Zylinder, der sich entlang seinem Umfang aufgrund der Lorentzkontraktion kontrahieren sollte, während sein Radius konstant bleibt. Die Grafik zeigt Maßstäbe die im Laborsystem ruhen, so wie Maßstäbe die mit dem Zylinder rotieren und deshalb relativ zum Laborsystem kontrahiert werden. |
| Tarih | |
| Kaynak | Yükleyenin kendi çalışması |
| Yazar | Geek3 |
| Diğer sürümler |
|
Source code
The image is created by the following source-code. Requirements:
python source code:
#!/usr/bin/python
# -*- coding: utf8 -*-
try:
import svgwrite as svg
except ImportError:
print 'You need to install svgwrite: http://pypi.python.org/pypi/svgwrite/'
exit(1)
from math import *
size = 220, 180
rx, ry = size[0] / 2 - 3, 50
v = float(ry) / float(rx)
l = 40
lw = 2
# document
doc = svg.Drawing('ehrenfest-paradox-disk.svg', size=size)
doc['stroke-width'] = lw
doc['fill'] = 'white'
doc['stroke'] = 'black'
doc['stroke-linejoin'] = 'miter'
# background
doc.add(doc.rect(id='background', insert=(0, 0), size=size, stroke='none'))
# disk
grad = doc.defs.add(doc.linearGradient(id='grad', start=('0%',0), end=('100%',0), gradientUnits='objectBoundingBox'))
grad.add_stop_color(offset=0, color='#F7F7F7')
grad.add_stop_color(offset=0.5, color='#DDD')
grad.add_stop_color(offset=1, color='#999')
disk = doc.add(doc.g(id='disk', transform='translate(' + str(size[0]/2) + ',' + str(ry+3) + ')'))
path = 'M ' + str(-rx) + ',0 V ' + str(l)
path += ' A ' + str(rx) + ',' + str(ry) + ' 0 1 0 ' + str(rx) + ',' + str(l)
path += ' V 0 Z'
disk.add(doc.path(d=path, fill='url(#grad)', stroke_linejoin='bevel'))
disk.add(doc.ellipse(center=(0, 0), r=(rx, ry), fill='#D8D8D8'))
disk.add(doc.ellipse(center=(0, 0), r=(2, 2.0*v), fill='black'))
radius_angle = radians(-40.0)
csr = cos(radius_angle), sin(radius_angle)
disk.add(doc.line(start=(0,0), end=(rx*csr[0], ry*csr[1]),
stroke_width=lw*sqrt(csr[0]**2 + (v*csr[1])**2)))
# round arrow
ar, aw, ah, ab, al, a0, a1 = 0.7*rx, 7, 2, 1, 3, radians(160), radians(100)
apath = 'M ' + str(ar*cos(a0)) + ',' + str(ar*sin(a0))
apath += ' A %f,%f 0 0 0 %f,%f' % (ar, ar, ar*cos(a1), ar*sin(a1))
arrowhead = doc.defs.add(doc.marker(id='arrowhead', orient='auto', overflow='visible'))
arrowhead.add(doc.path(fill='black', stroke='none',
d='M 0.0,0.0 L %f,%f L %f,0 L %f,%f L 0,0 z'%(-ab, -ah, al, -ab, ah)))
arrow = doc.path(d=apath, fill='none', stroke_width=aw, transform='scale(1,' + str(v) + ')')
arrow['marker-end'] = arrowhead.get_funciri()
disk.add(arrow)
# ruler
ruler = doc.defs.add(doc.g(id='ruler'))
rw, rh, rn = 32, 14, 4
ruler.add(doc.path(d='M 0,0 H %f V %f H 0 V 0 Z'%(rw+3, rh),
fill='white', stroke='none'))
squares = ''
for i in range(rn/2):
squares += 'M %f,0 H %f V %f H %f V 0 Z '%(i*rw*2./rn, (1+i*2.)*rw/rn, rh, i*rw*2./rn)
ruler.add(doc.path(d=squares, fill='red', stroke='none'))
ruleredge = 'M %f,0 H %f V %f H 0 V 0 H %f V %f'%(rw, 3+rw, rh, rw, rh)
for i in range(1, rn):
ruleredge += ' M %f,0 V %f'%(i*rw/float(rn), rh/2.)
ruler.add(doc.path(d=ruleredge, fill='none', stroke='black', stroke_width=lw, stroke_linecap='round'))
rulers = doc.add(doc.g(id='rulers'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.89, 0.42, 0, 1, 17, 134)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(1.00, 0.16, 0, 1, 54, 150)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(1.00, 0.00, 0, 1, 95, 156)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.53, 0.33, 0, 1, 16.53, 91)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.57, 0.19, 0, 1, 39, 104)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.60, 0.10, 0, 1, 63, 112)'))
doc.add(doc.path(d='M 16.5,106 V 133', fill='none', stroke_width=1, stroke_dasharray='4,2'))
doc.add(doc.path(d='M 84.5,130 V 154', fill='none', stroke_width=1, stroke_dasharray='4,2'))
# text
doc.add(doc.path(id='omega', stroke='none', fill='black',
transform='translate(70,70) scale(0.03,-0.03)',
d='M 13 0 m 251 82 c 9 -63 43 -93 94 -93 c 59 0 113 38 153 93 c 75 104 94 \
255 94 289 c 0 71 -37 71 -43 71 c -25 0 -50 -26 -50 -48 c 0 -13 6 -19 15 -27 \
c 32 -33 35 -65 35 -87 c 0 -85 -85 -219 -190 -219 c -9 0 -37 0 -55 23 c -12 \
16 -20 35 -20 55 c 0 3 0 5 6 16 c 19 45 33 100 33 113 c 0 12 -7 23 -21 23 c \
-11 0 -20 -9 -28 -25 c -2 -5 -14 -49 -21 -101 c -2 -18 -2 -20 -9 -27 c -44 \
-61 -90 -77 -124 -77 c -66 0 -88 55 -88 114 c 0 75 37 158 84 225 c 10 14 10 \
16 10 19 c 0 8 -6 12 -12 12 c -16 0 -62 -88 -76 -120 c -37 -89 -38 -171 -38 \
-180 c 0 -80 30 -142 106 -142 c 65 0 113 46 145 93 z'))
doc.add(doc.path(id='r', stroke='none', fill='black',
transform='translate(152,60) scale(0.03,-0.03)',
d='M 29 0 m 59 59 c -3 -15 -9 -38 -9 -43 c 0 -18 14 -27 29 -27 c 12 0 30 8 \
37 28 c 2 4 36 140 40 158 c 8 33 26 103 32 130 c 4 13 32 60 56 82 c 8 7 37 33 \
80 33 c 26 0 41 -12 42 -12 c -30 -5 -52 -29 -52 -55 c 0 -16 11 -35 38 -35 c \
27 0 55 23 55 59 c 0 35 -32 65 -83 65 c -65 0 -109 -49 -128 -77 c -8 45 -44 \
77 -91 77 c -46 0 -65 -39 -74 -57 c -18 -34 -31 -94 -31 -97 c 0 -10 10 -10 12 \
-10 c 10 0 11 1 17 23 c 17 71 37 119 73 119 c 17 0 31 -8 31 -46 c 0 -21 -3 \
-32 -16 -84 z'))
doc.save()
Lisanslama
Ben, bu işin telif sahibi, burada işi aşağıdaki lisanslar altında yayımlıyorum:
|
Bu belgenin GNU Özgür Belgeleme Lisansı, Sürüm 1.2 veya Özgür Yazılım Vakfı tarafından yayımlanan sonraki herhangi bir sürüm şartları altında bu belgenin kopyalanması, dağıtılması ve/veya değiştirilmesi için izin verilmiştir;
Değişmeyen Bölümler, Ön Kapak Metinleri ve Arka Kapak Metinleri yoktur. Lisansın bir kopyası GNU Özgür Belgeleme Lisansı sayfasında yer almaktadır. |
Bu dosya, Creative Commons Atıf 3.0 Uluslararası lisansı ile lisanslanmıştır
- Şu seçeneklerde özgürsünüz:
- paylaşım – eser paylaşımı, dağıtımı ve iletimi
- içeriği değiştirip uyarlama – eser adaptasyonu
- Aşağıdaki koşullar geçerli olacaktır:
- atıf – Esere yazar veya lisans sahibi tarafından belirtilen (ancak sizi ya da eseri kullanımınızı desteklediklerini ileri sürmeyecek bir) şekilde atıfta bulunmalısınız.
İstediğiniz lisansı seçebilirsiniz.
Dosya geçmişi
Dosyanın herhangi bir zamandaki hâli için ilgili tarih/saat kısmına tıklayın.
| Tarih/Saat | Küçük resim | Boyutlar | Kullanıcı | Yorum | |
|---|---|---|---|---|---|
| güncel | 01.35, 21 Ocak 2013 | | 220 × 180 (4 KB) | wikimediacommons>Geek3 | {{Information |Description ={{en|1=Ehrenfest paradox illustration}} |Source ={{own}} |Author =Geek3 |Date ={{Date|2013|01|21}} |Permission = |other_versions = }} |
Dosya kullanımı
Aşağıdaki sayfa bu dosyayı kullanmaktadır:
