Kontür integrali yöntemleri

Karmaşık analizde kontür integrali veya kontür integrali almak karmaşık düzlemdeki yollar boyunca belli integralleri bulmak için kullanılan bir yöntemdir.

Kontür integralinin karmaşık analizin bir metodu olan kalıntı hesabıyla yakın bir ilişkisi vardır.

Kontür integrallerinin bir kullanımı da halihazırdaki gerçel değişken yöntemleriyle bulunamayan gerçel eksendeki integralleri bulmaktır.

Kontür integrali yöntemleri şunları içerir:

• Karmaşık değerli bir fonksiyonun karmaşık düzlemdeki bir eğri (kontür) boyunca integralinin dolaysız bulunması
• Cauchy integral formülünün uygulanması
• Kalıntı teoreminin uygulanması

Bu integralleri veya toplamları bulmak amacıyla, bir yöntem veya bu yöntemlerin bir kombinasyonu veya çeşitli limit alma süreçleri kullanılabilir.

Dolaysız yöntemler

Dolaysız yöntemler, integralin, çok değişkenli hesaptaki integralleri hesaplamaya yarayan yöntemlere benzer yöntemlerle hesaplanmasını içerir. Bu da şu yöntemleri kullanmamız anlamına gelmektedir:

• Kontürü parametrize etme (parametrizasyon)
• Kontür gerçel değişkenli, karmaşık değerli, türevlenebilir bir fonksiyon tarafından parametrize edilir veya kontür parçalara bölünüp ayrı ayrı parametrize edilir.
• Parametrizasyonun integrand içine konulması
• Parametrizasyonun integrand içine konulması integrali bir gerçel değişkenli integrale dönüştürecektir.
• İntegral gerçel değişkenli integralde kullanılan yönteme benzer bir metotla bulunur.

Örnek

Karmaşık analizdeki temel sonuçlardan birisi de z⁻¹ in birim çember C etrafındaki (veya 0 etrafındaki herhangi bir Jordan eğrisi boyunca) integralinin 2πi olmasıdır. Şimdi

${\oint }_C\frac{1}{z}dz$

integralini bulalım.

Bu integrali bulmak için, kontür olarak γ(t) = e^it, t ∈ [0, 2π] ile parametrize edebileceğimiz |z| = 1 birim çemberini kullanıyoruz. γ'(t) = ie^it olduğunu gözlemleyip, bunu da z için yerine koyarsak

$\begin{array}{cc}{\oint }_C\frac{1}{z}dz& =\underset{0}{\overset{2\pi }{\int }}\frac{1}{e^{it}}i{e}^{it}dt=i\underset{0}{\overset{2\pi }{\int }}{e}^{-it}{e}^{it}dt=i\underset{0}{\overset{2\pi }{\int }}1dt\\ & =[t{]}_0^{2\pi }i=(2\pi -0)i=2\pi i\end{array}$

elde ederiz ki bu da integralin değeridir.

İntegral teoremlerinin uygulanması

İntegral teoremlerinin uygulanması genelde kontür integrallerini bir kontür boyunca bulmak için kullanılır. Bu da gerçel değerli integralin hesaplanmasının bir kontür integralini hesaplamayla aynı zamanda yapıldığı anlamına gelir.

Cauchy integral teoremi veya kalıntı teoremi gibi integral teoremler, genellikle şu yöntemde kullanılır:

• Belli bir kontür seçilir:

Kontür seçilir. Öyle ki, kontür karmaşık düzlemin gerçel değerli integrali tanımlayan bir parçasını takip eder ve ayrıca integrandın da tekilliklerini içerir. Böylece, Cauchy integral formülü veya kalıntı teoreminin kullanımı mümkün olur.

• Cauchy-Goursat teoreminin uygulanması

İntegral her kutup etrafındaki küçük bir çember etrafında alınan bir integral haline gelir.

• Cauchy integral teoremi veya kalıntı teoreminin uygulanması

Bu integral formülünün uygulanması kontürün tümü üzerindeki integralin değerini verir.

• Kontürün gerçel ve sanal kısımları olan başka bir kontüre bölünmesi.

Tüm kontür karmaşık düzlemin parçasını takip eden bir integrale bölünür ki bu kontür de daha önce seçilmiş gerçel değerli integrali (buna R diyelim) ve karmaşık düzlemi kesen integrali (buna da I diyelim) açıklar. Tüm kontür üzerinde alınan integral bu parçalanmış her kontür üzerindeki integrallerin bir toplamıdır.

• Karmaşık düzlemi kesen integralin gösteriminin toplamda bir rolü yoktur.

Eğer I integralinin sıfır olduğu gösterilebilirse veya aranan gerçek değerli integral düzensiz integral ise ve sonra yukarıdaki gibi açıklanan I integralinin 0'a gittiğini gösterebilirsek, R boyuncaki integral R+I kontürü boyuncaki integrale gidecektir.

• Sonuç

Yukarıdaki adımı gösterebilirsek, o zaman R 'yi, gerçel değerli integrali, dolaysız bir şekilde hesaplayabiliriz.

Örnek (I)

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{1}{(x^2+1{)}^2}dx$ integralini ele alalım.

the contour

Bu integrali bulmak için karmaşık değerli, i ve -i noktalarında tekillikleri olan

$f(z)=\frac{1}{(z^2+1{)}^2}$

fonksiyonuna bakıyoruz. Bununla birlikte, gerçel değerli integrali çevreleyecek kontürü de seçmek istiyoruz; böylece solda gösterilen ve uzattığımızda tüm gerçel ekseni içerecek (a sonsuza gidecek) yarım çemberi seçiyoruz. Bu kontüre C diyelim.

Şimdi, ilerlemek için kullanabileceğimiz iki adım var: Cauchy integral formülü veya kalıntılar yöntemi.

• Cauchy integral teoreminin kullanılması

$f(z)=\frac{1}{(z^2+1{)}^2}=\frac{1}{(z+i{)}^2(z-i{)}^2}.$

olduğunu gözlemleyelim. Kontür içindeki tek tekilli i 'deki tekillik olduğu için,

$f(z)=\frac{\frac{1}{(z+i{)}^2}}{(z-i{)}^2}$

yazabiliriz ki bu da fonksiyonu formülü dolaysız bir şekilde uygulayacak biçime getirir.

O zaman Cauchy integral formülü ile

${\oint }_{C}f(z)dz={\oint }_C\frac{1}{(z^2+1{)}^2}dz={\oint }_C\frac{\frac{1}{(z+i{)}^2}}{(z-i{)}^2}dz=2\pi i\frac{d}{dz}{\left(\frac{1}{(z+i{)}^2})\right|}_{z=i}$

$=2\pi i{\left(\frac{-2}{(z+i{)}^3}\right)|}_{z=i}=2\pi i(-i/4)=\frac{\pi }{2}$

(Yukarıdaki adımlarda birinci türevi alıyoruz çünkü kutup ikinci bir mertebeden bir kutuptur. Yani; (z - i) 'nin ikinci kuvveti olduğu için ƒ(z) 'nin ilk türevini alıyoruz. Eğer (z - i) 'nin üçüncü kuvveti alınsaydı, o zaman ikinci türevi alacaktık vs. (z - i) 'nin birinci kuvveti ise sıfırıncı mertebeden türeve karşılık gelir ki bu da ƒ(x) 'in kendisidir.)

Yarı çemberin yayına A dersek, A üzerindeki integralin a sonsuza gittikçe 0'a gittiğini göstermemiz gerekir. L, A 'nın uzunluğuysa ve M, |f(z)| üzerinde bir üst sınırsa, o zaman tahmin lemmasını kullanarak

$|\underset{A}{\int }f(z)dz|\le ML$

yazılabilir. Şimdi,

$\underset{A}{\int }f(z)dz\le \frac{a\pi }{(a^2+1{)}^2}\to 0,a\to \mathrm{\infty }\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{n}$

Böylece;

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(z)dz=\frac{\pi }{2}.◻$

Kalıntılar yönteminin kullanılması

f(z) 'nin düşünmemiz gereken tek tekllik olan i civarındaki Laurent serisini ele alalım. O zaman,

$f(z)=\frac{-1}{4(z-i{)}^2}+\frac{-i}{4(z-i)}+\frac{3}{16}+\frac{i}{8}(z-i)+\frac{-5}{64}(z-i{)}^2+\cdots$

(Laurent serisi maddesinden bu çıkarım için örneğe bakınız.)

Kalıntının ufak bir incelemeyle -i/4 olacağı açıktır (bunu görmek için, yukarıdaki eşitliğin z - i ile çarpıldığını; sonra her iki tarafın da Cauchy integral formülü ile integralinin alındığını varsayalım. Sadece ikinci terimin integralinin sonucu 0 olmayan bir nicelik verecektir.). O zaman kalıntı teoremi ile şunu elde ederiz:

${\oint }_{C}f(z)dz={\oint }_C\frac{1}{(z^2+1{)}^2}dz=2\pi i{\mathrm{R}\mathrm{e}\mathrm{s}}_{z=i}f=2\pi i(-i/4)=\frac{\pi }{2}◻$

Yarı çemberin yayına A dersek, A üzerindeki integralin a sonsuza gittikçe 0'a gittiğini göstermemiz gerekir. L, A 'nın uzunluğuysa ve M, |f(z)| üzerinde bir üst sınırsa, o zaman tahmin lemmasını kullanarak

$|\underset{A}{\int }f(z)dz|\le ML$

yazılabilir. Şimdi,

$\underset{A}{\int }f(z)dz\le \frac{a\pi }{(a^2+1{)}^2}\to 0,a\to \mathrm{\infty }\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{n}$

Böylece;

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(z)dz=\frac{\pi }{2}.◻$

Böylece aynı sonucu elde etmiş olduk.

Kontür notu

Bir yandan, diğer tekilliği, yani -i 'yi, de çevreleyecek bir yarım çember alınıp alınamayacağı sorusu da sorulabilir. Gerçel eksendeki integrali doğru yönde elde etmek için, kontür saat yönünde olmalıdır; yani integralin tamamıyla işaretini değiştiren negatif yönde olmalıdır.

Bu serilerle kalıntılar yönteminin kullanımını etkilemez.

Örnek(II) – Cauchy dağılımı

Olasılık kuramında Cauchy dağılımının karakteristik fonksiyonunun skaler bir katı olarak karşımıza çıkan

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{e^{itx}}{x^2+1}dx$

the contour

integrali basit hesabın tekniklerine karşı koymaktadır. Bu integrali, gerçel doğru üzerinde -a 'dan a 'ya ve daha sonra da 0 merkezli yarım çember üzerinde saat yönünün tersine a 'dan -a 'ya giden bir C kontürü boyuncaki kontür integrallerinin limiti olarak bulacağız. a, 1'den büyük olsun böylece sanal birim i eğrinin iç tarafnda kalsın. O zaman kontür integrali şudur:

$\underset{C}{\int }\frac{e^{itz}}{z^2+1}dz.$

e^itz bir tam fonksiyon olduğundan (karmaşık düzlemin herhangi bir noktasında tekilliği yok), bu fonksiyonun tekillikleri payda z² + 1 'in 0 olduğu yerlerde olacaktır. z² + 1 = (z + i)(z - i) olduğu için, bu da sadece z = i veya z = -i 'de olacaktır. Bu noktalardan sadece bir tanesi bu kontürün sınırladığı bölgede kalacaktır. f(z) 'nin z = i 'deki kalıntısı şu şekildedir:

$\underset{z\to i}{\lim }(z-i)f(z)=\underset{z\to i}{\lim }(z-i)\frac{e^{itz}}{z^2+1}=\underset{z\to i}{\lim }(z-i)\frac{e^{itz}}{(z-i)(z+i)}$

$=\underset{z\to i}{\lim }\frac{e^{itz}}{z+i}=\frac{e^{iti}}{i+i}=\frac{e^{-t}}{2i}.$

Kalıntı teoremine göre, o zaman şunu elde ederiz.

$\underset{C}{\int }f(z)dz=2\pi i\cdot {\mathrm{Res}}_{z=i}f(z)=2\pi i\frac{e^{-t}}{2i}=\pi e^{-t}.$

C kontürü bir "doğru"ya ve bir de eğri bir yaya parçalanabilir. Böylece

$\underset{\text{dogru}}{\int }+\underset{\text{yay}}{\int }=\pi e^{-t}$

olur ve bu yüzden

$\underset{-a}{\overset{a}{\int }}=\pi e^{-t}-\underset{\text{yay}}{\int }$

olur. Eğer t > 0 ise, o zaman

$\underset{\text{yay}}{\int }\frac{e^{itz}}{z^2+1}dz\to 0\text{,}a\to \mathrm{\infty }\text{iken}.$

Bu yüzden, eğer t > 0 ise, o zaman

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{e^{itz}}{z^2+1}dz=\pi e^{-t}.$

i yerine -i 'yi dolanan bir yay durumundaki benzer bir tartışma eğer t < 0 ise, o zaman

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{e^{itz}}{z^2+1}dz=\pi e^t$

olduğunu gösterir ve sonuç olarak şunu elde ederiz:

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{e^{itz}}{z^2+1}dz=\pi e^{-\left|t\right|}.◻$

(t = 0 ise, o zaman integral gerçel-değerli hesabın yöntemleriyle çözülebilecek duruma gelir ve değeri de π olur.)

Örnek (III) – trigonometrik integraller

Trigonometrik fonksiyonları içeren integrallere belli yerine koymalar yapılarak bu integraller karmaşık değişkenli rasyonel fonksiyonların integrallerine dönüştürülebilir ve böylece yukarıdaki teknikler integrali bulmak için kullanılabilir.

Örnek olarak şu integrali ele alalım:

$\underset{-\pi }{\overset{\pi }{\int }}\frac{1}{1+3(\cos t{)}^2}dt.$

z = e^it yerine koymasını yapabilmeyi arıyoruz.

Şimdi, şunları hatırlayalım:

$\cos t=\frac{1}{2}(e^{it}+e^{-it})=\frac{1}{2}(z+\frac{1}{z})$

ve

$\frac{dz}{dt}=iz,dt=\frac{dz}{iz}.$

C 'yi birim çember alarak ve yerine koymayı yaparak şunu elde ederiz:

${\oint }_C\frac{1}{1+3(\frac{1}{2}(z+\frac{1}{z}){)}^2}\frac{dz}{iz}$

$={\oint }_C\frac{1}{1+\frac{3}{4}(z+\frac{1}{z}{)}^2}\frac{1}{iz}dz={\oint }_C\frac{-i}{z+\frac{3}{4}z(z+\frac{1}{z}{)}^2}dz=-i{\oint }_C\frac{1}{z+\frac{3}{4}z(z^2+2+\frac{1}{z^2})}dz$

$=-i{\oint }_C\frac{1}{z+\frac{3}{4}(z^3+2z+\frac{1}{z})}dz=-i{\oint }_C\frac{1}{\frac{3}{4}{z}^3+\frac{5}{2}z+\frac{3}{4z}}dz$

$=-i{\oint }_C\frac{4}{3z^3+10z+\frac{3}{z}}dz=-4i{\oint }_C\frac{1}{3z^3+10z+\frac{3}{z}}dz$

$=-4i{\oint }_C\frac{z}{3z^4+10z^2+3}dz.$

Cauchy integral formülünü kullanıyoruz. Paydayı çarpanlarına ayıralım:

$=-4i{\oint }_C\frac{z}{3z^4+10z^2+3}dz=-4i{\oint }_C\frac{z}{3(z^2+3)(z^2+1/3)}dz$

$=-4i{\oint }_C\frac{z}{3(z+\sqrt{3}i)(z-\sqrt{3}i)(z+\sqrt{\frac{1}{3}}i)(z-\sqrt{\frac{1}{3}}i)}dz$

$=-\frac{4}{3}i{\oint }_C\frac{z}{(z+\sqrt{3}i)(z-\sqrt{3}i)(z+\sqrt{\frac{1}{3}}i)(z-\sqrt{\frac{1}{3}}i)}dz.$

O zaman göz önüne alınması gereken tekillikler 3^-1/2i ve -3^-1/2i 'de olur. O zaman integral şu hale gelir:

$=-\frac{4}{3}i{\oint }_{C_1}\frac{\frac{z}{(z+\sqrt{3}i)(z-\sqrt{3}i)(z+\sqrt{\frac{1}{3}}i)}}{(z-\sqrt{\frac{1}{3}}i)}dz+-\frac{4}{3}i{\oint }_{C_2}\frac{\frac{z}{(z+\sqrt{3}i)(z-\sqrt{3}i)(z-\sqrt{\frac{1}{3}}i)}}{(z+\sqrt{\frac{1}{3}}i)}$

Burada C₁, 3^-1/2i etrafındaki küçük çemberdir ve C₂, -3^-1/2i etrafındaki büyük çemberdir. Şimdi formülü uygulayabiliriz:

$=-\frac{4}{3}i(2\pi i{\left(\frac{z}{(z+\sqrt{3}i)(z-\sqrt{3}i)(z+\sqrt{\frac{1}{3}}i)}\right)|}_{z=\sqrt{\frac{1}{3}}i}$

$+2\pi i{\left(\frac{z}{(z+\sqrt{3}i)(z-\sqrt{3}i)(z-\sqrt{\frac{1}{3}}i)}\right)|}_{z=-\sqrt{\frac{1}{3}}i})$

$=-\frac{4}{3}i(2\pi i\left(\frac{\sqrt{\frac{1}{3}}i}{(\sqrt{\frac{1}{3}}i+\sqrt{3}i)(\sqrt{\frac{1}{3}}i-\sqrt{3}i)(\sqrt{\frac{1}{3}}i+\sqrt{\frac{1}{3}}i)}\right)$

$+2\pi i\left(\frac{-\sqrt{\frac{1}{3}}i}{(-\sqrt{\frac{1}{3}}i+\sqrt{3}i)(-\sqrt{\frac{1}{3}}i-\sqrt{3}i)(-\sqrt{\frac{1}{3}}i-\sqrt{\frac{1}{3}}i}\right))$

$=-\frac{4}{3}i(2\pi i\left(\frac{\sqrt{\frac{1}{3}}i}{(\frac{4}{\sqrt{3}}i)(-\frac{2}{\sqrt{3}}i)(\frac{2}{\sqrt{3}}i)}\right)+2\pi i\left(\frac{-\sqrt{\frac{1}{3}}i}{(\frac{2}{\sqrt{3}}i)(-\frac{4}{\sqrt{3}}i)(-\frac{2}{\sqrt{3}}i)}\right))$

$=-\frac{4}{3}i(2\pi i\left(\frac{\sqrt{\frac{1}{3}}i}{i(\frac{4}{\sqrt{3}})(\frac{2}{\sqrt{3}})(\frac{2}{\sqrt{3}})}\right)+2\pi i\left(\frac{-\sqrt{\frac{1}{3}}i}{-i(\frac{2}{\sqrt{3}})(\frac{4}{\sqrt{3}})(\frac{2}{\sqrt{3}})}\right))$

$=-\frac{4}{3}i(2\pi i\left(\frac{\sqrt{\frac{1}{3}}}{(\frac{4}{\sqrt{3}})(\frac{2}{\sqrt{3}})(\frac{2}{\sqrt{3}})}\right)+2\pi i\left(\frac{\sqrt{\frac{1}{3}}}{(\frac{2}{\sqrt{3}})(\frac{4}{\sqrt{3}})(\frac{2}{\sqrt{3}})}\right))$

$=-\frac{4}{3}i(2\pi i\left(\frac{\sqrt{\frac{1}{3}}}{\frac{16}{3\sqrt{3}}}\right)+2\pi i\left(\frac{\sqrt{\frac{1}{3}}}{\frac{16}{3\sqrt{3}}}\right))$

$=-\frac{4}{3}i(2\pi i\left(\frac{3}{16}\right)+2\pi i\left(\frac{3}{16}\right))=-\frac{4}{3}i\left(\pi i(\frac{3}{8}+\frac{3}{8})\right)=\frac{4}{3}\left(\frac{3}{4}\right)\pi =\pi .◻$

Örnek (IIIa) – trigonometrik integraller, genel prosedür

Yukarıdaki yöntem, $P$ ve $Q$ 'nun polinom olduğu

$\underset{0}{\overset{2\pi }{\int }}\frac{P(\sin (t),\sin (2t),\dots ,\cos (t),\cos (2t)\dots )}{Q(\sin (t),\sin (2t),\dots ,\cos (t),\cos (2t)\dots )}dt$

tipindeki bütün integrallere; yani trigonometrik terimler halindeki rasyonel fonksiyonların integrallerine uygulanabilir.

Burada yapılan hile $z=\exp (it)$, $dz=i\exp (it)dt$ yerine koyması yapmaktır. Bu yüzden

$\frac{1}{iz}dz=dt$

elde edilir. Bu yerine koyma $[0,2\pi ]$ aralığını birim çembere gönderir. Dahası,

$\sin (kt)=\frac{\exp (ikt)-\exp (-ikt)}{2i}=\frac{z^k-z^{-k}}{2i}$

ve

$\cos (kt)=\frac{\exp (ikt)+\exp (-ikt)}{2}=\frac{z^k+z^{-k}}{2}$

olur ve böylece yerine koyma işleminden $z$ değişkenli bir $f(z)$ rasyonel fonksiyonu ortaya çıkar ve integral

${\oint }_{|z|=1}f(z)\frac{1}{iz}dz$

haline gelir ki bu da birim çember içindeki $f(z)$'nin kalıntılarının toplanmasıyla hesaplanır.

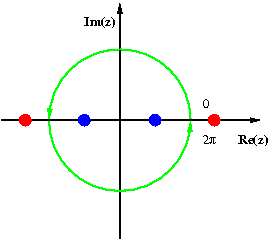
Sağdaki resim bunu şimdi hesaplayacağımız

$I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{1+\sin (t{)}^2}dt$

için göstermektedir. Birinci adım şudur:

$I=\frac{1}{4}\underset{0}{\overset{2\pi }{\int }}\frac{1}{1+\sin (t{)}^2}dt.$

Yerine koymayla

$\frac{1}{4}{\oint }_{|z|=1}\frac{4iz}{z^4-6z^2+1}dz={\oint }_{|z|=1}\frac{iz}{z^4-6z^2+1}dz$

elde edilir. Bu fonksiyonun kutupları $1\pm \sqrt{2}$ ve $-1\pm \sqrt{2}$ 'dedir. Bunlardan $1+\sqrt{2}$ ve $-1-\sqrt{2}$ birim çemberin dışında yer alırken (kırmızı ile gösterilmiştir ancak ölçekli gösterilmemiştir), $1-\sqrt{2}$ ve $-1+\sqrt{2}$ birim çemberin içinde yer alır (mavi ile gösterilmiştir). Karşılık gelen kalıntıların her ikisi de $-\frac{\sqrt{2}}{16}i$ 'ye eşittir böylece integralin değeri

$I=2\pi i2(-\frac{\sqrt{2}}{16}i)=\pi \frac{\sqrt{2}}{4}$

olur.

Örnek (IV) – dallanma kesikleri

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}dx$

integraline bakalım. Şu karmaşık integrali formüle ederek başlayabiliriz:

$\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz=I.$

Yine ilişkin kalıntıları elde etmek için Cauchy integral formülü veya kalıntı teoremini kullanabiliriz. Ancak, burada dikkat edilmesi gereken nokta z^1/2=e^1/2.Log(z) olmasıdır böylece z^1/2 'nin dallanma kesiği vardır. Bu da seçtiğimiz C kontürünü etkiler. Normalde, logaritma dallanma kesiği negatif gerçel eksen olarak tanımlanır; ancak, bu da integralin hesabını biraz daha karışık hale getirir. Bu yüzden, dallanma kesiğini pozitif eksen olarak alıyoruz.

O zaman, orijinde ε yarıçaplı bir çemberle başlayan, bu çemberden uzayarak pozitif gerçel eksene oldukça yakın ve paralel olan ancak eksene dokanmayan sonra da saat yönünün tersi yönde ufak çemberden daha büyük yarıçapta bir döngü (neredeyse tam bir çember) yapıp tekrar pozitif eksene parallel bir şekilde (ancak bu sefer negatif eksen yönünde) ufak çemberle birleşen ve anahtar deliği kontürü adı verilen kontürü kullanalım.

z = -2 ve z = -4 büyük çemberin içindeler. Bunlar kalan iki kutuptur ve integrandın paydasını çarpanlara ayırarak elde edilebilir. z = 0 'daki kutuptan orijin etrafında tur yapılarak kaçınılmıştır. Şablon:Temiz

γ, ε yarıçaplı ufak çember, Γ ise R yarıçaplı büyük çember olsun. O zaman,

$\begin{array}{ccc}\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz& =& \underset{\epsilon }{\overset{R}{\int }}\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{\mathrm{\Gamma }}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{R}{\overset{\epsilon }{\int }}\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{\gamma }{\int }\frac{\sqrt{z}}{z^2+6z+8}dz.\end{array}$

z^1/2 = e^{1/2 Log(z)} olduğu için, dallanma kesiğinin üzerindeki kontür üzerinde, γ boyunca argumentte 2π kazanılmıştır (Euler Özdeşliğiyle, $e^{i\pi }$ birim vektörü temsil eder ki bu yüzden log olarak $i\pi$ 'ye sahiptir. z 'nin argumentinden de kastedilen bu $\pi$'dir. 1/2 katsayısı ise bizi 2 çarpı $\pi$ yazmaya zorlamaktadır.); böylece

$\underset{R}{\overset{\epsilon }{\int }}\frac{\sqrt{z}}{z^2+6z+8}dz=\underset{R}{\overset{\epsilon }{\int }}\frac{e^{\frac{1}{2}\mathrm{L}\mathrm{o}\mathrm{g}(z)}}{z^2+6z+8}dz=\underset{R}{\overset{\epsilon }{\int }}\frac{e^{\frac{1}{2}(\log |z|+i\arg z)}}{z^2+6z+8}dz$

$=\underset{R}{\overset{\epsilon }{\int }}\frac{e^{\frac{1}{2}\log |z|}{e}^{1/2(2\pi i)}}{z^2+6z+8}dz=\underset{R}{\overset{\epsilon }{\int }}\frac{e^{\frac{1}{2}\log |z|}{e}^{\pi i}}{z^2+6z+8}dz$

$=\underset{R}{\overset{\epsilon }{\int }}\frac{-\sqrt{x}}{x^2+6x+8}dx=-\underset{\epsilon }{\overset{R}{\int }}\frac{-\sqrt{x}}{x^2+6x+8}dx$

basitleştirerek,

$=\underset{\epsilon }{\overset{R}{\int }}\frac{\sqrt{x}}{x^2+6x+8}dx,$

ve sonra

$\begin{array}{ccc}\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz& =& \underset{\epsilon }{\overset{R}{\int }}\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{\mathrm{\Gamma }}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{\epsilon }{\overset{R}{\int }}\frac{\sqrt{z}}{z^2+6z+8}dz\\ & +& \underset{\gamma }{\int }\frac{\sqrt{z}}{z^2+6z+8}dz\end{array}$

elde edilir.

Γ ve γ üzerindeki her iki integralin de ε sıfıra ve R sonsuza gittikçe sıfıra gittiği yukarıda bir tahmin tartışması yapılarak gösterilebilir. Bu yüzden, o zaman,

$\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}dz=2\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}dx.$

Kalıntı teoremi veya Cauchy integral formülü kullanılarak (iki basit kontür integralinin toplamını elde etmek için ilk önce kısmi kesirler yöntemini kullanarak), aşağıdaki elde edilir.

$\pi i(\frac{i}{\sqrt{2}}-i)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}dx=\pi (1-\frac{1}{\sqrt{2}}).◻$

Örnek (V) – logaritmalar ve sonsuzdaki kalıntı

$I=\underset{0}{\overset{3}{\int }}\frac{{(x^3(3-x))}^{1/4}}{5-x}dx$

integralini bulmaya çalışalım. Bu integrali bulmak için

$f(z)={(z^3(3-z))}^{1/4}$

fonksiyonunu incelememiz lazım. $f(z)$ 'yi inşa edeceğiz öyle ki $[0,3]$ aralığı üzerinde dallanma kesiği olacak (resimde kırmızı ile gösterilmiştir). Bunu yapmak içinse, logaritmanın iki tane dallanmasını seçiyoruz; yani

$(z^3{)}^{1/4}=z^{3/4}=\exp (3/4\log (z))\text{,}-\pi \le \arg (\log (z))<\pi$

ve

$(3-z{)}^{1/4}=\exp (1/4\log (3-z))\text{,}0\le \arg (\log (z))<2\pi .$

$z^{3/4}$ 'ün kesiği bu yüzden $(-\mathrm{\infty },0]$ aralığı olurken, $(3-z{)}^{1/4}$ 'ün kesiği $(-\mathrm{\infty },3]$ aralığı olur. Bu ikisinin çarpımının yani $f(z)$'nin kesiği $[0,3]$ olur çünkü $f(z)$ aslında $(-\mathrm{\infty },0)$ boyunca süreklidir. Bunun nedeni ise, $z=-r<0$ iken, kesiğe üstten yaklaşırsak, $f(z)$'nin şu değeri almasıdır:

$r^{3/4}\exp (3/4\pi i)(3+r{)}^{1/4}\exp (2/4\pi i)=r^{3/4}(3+r{)}^{1/4}\exp (5/4\pi i).$

Alttan yaklaşırsak, $f(z)$ şu değeri alır:

$r^{3/4}\exp (-3/4\pi i)(3+r{)}^{1/4}\exp (0/4\pi i)=r^{3/4}(3+r{)}^{1/4}\exp (-3/4\pi i).$

Ancak, $\exp (-3/4\pi i)=\exp (5/4\pi i)$ olduğu için kesiği geçerken bile süreklilik vardır. Bu da resimde $z^{3/4}$ ve $(3-z{)}^{1/4}$'te kullanılan logaritmanın argumentine karşılık gelen değerlerin etiketlendiği iki yönlü siyah çember ile gösterilmiştir.

Burada resimde yeşil renkle gösterilen kontürü kullanacağız. Bunu yapmak için, kesiğin hemen üstünde ve altında yer alan doğru parçaları boyunca $f(z)$'nin aldığı değerleri hesaplamamız gerekir. Üst parça boyunca, $f(z)$'nin aldığı değer şudur:

$r^{3/4}\exp (3/40\pi i)(3-r{)}^{1/4}\exp (2/4\pi i)=i{r}^{3/4}(3-r{)}^{1/4}$

Alt parça boyunca yine $f(z)$'nin aldığı değer şudur:

$r^{3/4}\exp (3/40\pi i)(3-r{)}^{1/4}\exp (0/4\pi i)=r^{3/4}(3-r{)}^{1/4}$

O zaman, $f(z)/(5-z)$'nin üst parça boyuncaki integrali limitte $-iI$ olurken, alt parça durumunda ise $I$ olur.

Eğer limitte iki yeşil çember üzerinde alınan integrallerin değerinin sıfır olduğunu gösterebilirsek, o zaman aynı zamanda Cauchy kalıntı teoremi ile $I$'nın değerini de elde etmiş oluruz. Yeşil çemberlerin yarıçapını $\rho$ ile gösterelim ve $\rho <1/1000$ olsun. $\rho \to 0$ iken ML-eşitsizliğini uygulayalım. Soldaki $C_L$ çemberi için şunu elde ederiz:

$\left|\underset{C_L}{\int }\frac{f(z)}{5-z}dz\right|\le 2\pi \rho \frac{{\rho }^{3/4}(3+1/1000{)}^{1/4}}{5-1/1000}\in 𝒪\left({\rho }^{7/4}\right)\to 0.$

Benzer bir şekilde, sağdaki $C_R$ çemberi için şunu elde ederiz:

$\left|\underset{C_R}{\int }\frac{f(z)}{5-z}dz\right|\le 2\pi \rho \frac{(3+1/1000{)}^{3/4}{\rho }^{1/4}}{2-1/1000}\in 𝒪\left({\rho }^{5/4}\right)\to 0.$

Şimdi Cauchy kalıntı teoremini kullanarak aşağıdaki eşitliği elde ederiz:

$(1-i)I=-2\pi i({\mathrm{R}\mathrm{e}\mathrm{s}}_{z=5}\frac{f(z)}{5-z}+{\mathrm{R}\mathrm{e}\mathrm{s}}_{z=\mathrm{\infty }}\frac{f(z)}{5-z}).$

Logaritmanın önceki dallanmasını kullanarak aşağıdaki ifade açıktır:

${\mathrm{R}\mathrm{e}\mathrm{s}}_{z=5}\frac{f(z)}{5-z}=-5^{3/4}\exp (1/4\log (-2)).$

Resimde kutup mavi ile gösterilmiştir. O zaman, değer de

$-5^{3/4}\exp (1/4(\log (2)+\pi i))=-\exp (1/4\pi i)5^{3/4}{2}^{1/4}$

şeklinde sadeleşir.

Sonsuzdaki kalıntı için ise şu formülü kullanıyoruz:

${\mathrm{R}\mathrm{e}\mathrm{s}}_{z=\mathrm{\infty }}h(z)={\mathrm{R}\mathrm{e}\mathrm{s}}_{z=0}-\frac{1}{z^2}h\left(\frac{1}{z}\right).$

Yerine koyarak,

$1/(5-1/z)=-z(1+5z+5^2{z}^2+5^3{z}^3+\cdots )$

ve

${(1/z^3(3-1/z))}^{1/4}=1/z(3z-1{)}^{1/4}=1/z\exp (1/4\pi i)(1-3z{)}^{1/4}$

eşitliklerini elde ederiz. Burada kullandığımız gerçek ise, logaritmanın ikinci dallanması için $-1=\exp (\pi i)$ olmasıdır. Sonra, binom açılımını kullanarak

$1/z\exp (1/4\pi i)(1-(\genfrac{}{}{0ex}{}{1/4}{1})3z+(\genfrac{}{}{0ex}{}{1/4}{2})3^2{z}^2-(\genfrac{}{}{0ex}{}{1/4}{3})3^3{z}^3+\cdots )$

elde ederiz. Sonuç ise,

${\mathrm{R}\mathrm{e}\mathrm{s}}_{z=\mathrm{\infty }}\frac{f(z)}{5-z}=\exp (1/4\pi i)(5-3/4)=\exp (1/4\pi i)17/4$

olur. Son olarak, $I$'nın değeri ise şu olur:

$I=-2\pi i\frac{\exp (1/4\pi i)}{1-i}(17/4-5^{3/4}{2}^{1/4})=-2\pi i{2}^{-1/2}i(17/4-5^{3/4}{2}^{1/4})$

yani

$I=\frac{\pi }{2\sqrt{2}}(17-5^{3/4}{2}^{9/4})=\frac{\pi }{2\sqrt{2}}(17-40^{3/4}).$

Ayrıca bakınız

• Cauchy integral formülü Bu integral teoreminin uygulanmasının bir örneği için
• Kalıntı (karmaşık analiz)
• Cauchy esas değeri
• Poisson integrali

Dış bağlantılar

• Örneklerin toplandığı bir site
• Kalıntı Hesabı Modülü, John H. Mathews tarafından

Bibliyografya

• Les-Mathematiques.net, Jean Jacquelin, Marko Riedel, Branche univalenteŞablon:Ölü bağlantı, Les-Mathematiques.net, Fransızca.
• Çeşitli yazarlar, sin límites ni cotas Şablon:Webarşiv, es.ciencia.matematicas, İspanyolca.