Toplanmış alan tablosu

Şablon:Ortala

Toplanmış alan tablosu, bir ızgaranın dikdörtgen bir alt kümesindeki değerlerin toplamını hızlı ve verimli bir şekilde oluşturmak için bir veri yapısı ve algoritmadır. Görüntü işleme alanında, bütünleşik görüntü (integral image) olarak da bilinir. 1984 yılında Frank Painter tarafından mipmap'lerle kullanılmak üzere bilgisayar grafiklerine tanıtıldı. Bilgisayarla görmede Lewis tarafından popüler hale getirildi ve ardından "bütünleşik görüntü" adı verildi. 2001'de Viola-Jones nesne algılama çerçevesinde belirgin bir şekilde kullanıldı. Tarihsel olarak, bu ilke, çok boyutlu olasılık dağılım fonksiyonları çalışmasında, yani ilgili kümülatif dağılım fonksiyonlarından 2D (veya ND) olasılıkların (olasılık dağılımının altındaki alan) hesaplanmasında çok iyi bilinmektedir.

Algoritma

Adından da anlaşılacağı gibi, herhangi bir noktadaki değer (x, y) toplanmış alan tablosundaki (x, y)’nin yukarısındaki ve solundaki, kendisi de dahil tüm piksellerin toplamıdır: $I(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}i(x^{\prime },y^{\prime })$

burada $i(x,y)$, (x, y) noktasındaki piksel değeridir.

Toplanmış alan tablosu, (x, y)’deki toplanmış alan tablosundaki değer yalnızca aşağıdaki ifade olduğundan, görüntü üzerinden tek bir geçişte verimli bir şekilde hesaplanabilir: $I(x,y)=i(x,y)+I(x,y-1)+I(x-1,y)-I(x-1,y-1)$ (Toplanmış matrisin sol üst köşeden hesaplandığına dikkat edin)

Şablon:Ortala

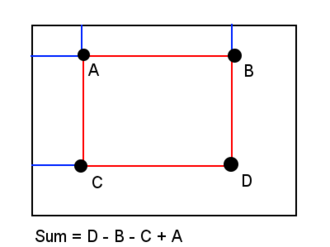
Toplanmış alan tablosu hesaplandıktan sonra, herhangi bir dikdörtgen alan üzerindeki yoğunlukların toplamını değerlendirmek, alan boyutuna bakılmaksızın tam olarak dört dizi referansı gerektirir. Yani, şekildeki gösterim üzerinden ifade edilirse, A = (x₀, y₀), B = (x₁, y₀), C = (x₀, y₁) ve D = (x₁, y₁), A, B, C ve D tarafından oluşturulan dikdörtgendeki i(x, y) toplamı aşağıdaki şekilde hesaplanır:

$\sum _{\begin{array}{c}{x}_0<x\le x_1\\ y_0<y\le y_1\end{array}}i(x,y)=I(D)+I(A)-I(B)-I(C)$

Genişlemeler

Bu yöntem doğal olarak sürekli alanlara genişletilir.

Yöntem, yüksek boyutlu görüntülere de genişletilebilir. Dikdörtgenin köşeleri $x^p$ ile $p$ içinde $\{0,1{\}}^d$, dikdörtgenin içerdiği görüntü değerlerinin toplamı aşağıdaki formülle hesaplanır:

$\sum _{p\in \{0,1{\}}^d}(-1{)}^{d-\Vert p{\Vert }_1}I(x^p)$

burada $I(x)$ bütünleşik görüntü, $x$ ve $d$ görüntü boyutudur. Gösterim $x^p$ örnekte $d=2$, $A=x^{(0,0)}$, $B=x^{(1,0)}$, $C=x^{(1,1)}$ ve $D=x^{(0,1)}$ ye karşılık gelir. Nörogörüntülemede görüntülerin boyutları vardır, örneğin; $d=3$ veya $d=4$, zaman damgalı voksel veya voksel kullanırken.

Bu yöntem, Phan ve diğerlerinin çalışmasında olduğu gibi yüksek dereceli bütünleşik görüntüye genişletilmiştir. görüntüdeki yerel bloğun standart sapmasını (varyans), çarpıklığını ve basıklığını hızlı ve verimli bir şekilde hesaplamak için iki, üç veya dört bütünleşik görüntü sağladı. Bu aşağıda detaylandırılmıştır:

Bir bloğun varyansını veya standart sapmasını hesaplamak için iki integral resme ihtiyacımız vardır:

$I(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}i(x^{\prime },y^{\prime })$

$I^2(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}{i}^2(x^{\prime },y^{\prime })$

Varyans aşağıdaki şekilde hesaplanır:

$\mathrm{Var}(X)=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2.$

$S_1$ ve $S_2$ sırasıyla $I$ ve $I^2$'nin $ABCD$ bloğun özetini göstersin. $S_1$ ve $S_2$ integral görüntü ile hızlı bir şekilde hesaplanır. Şimdi, varyans denklemini şu şekilde değiştirebiliriz:

$\mathrm{Var}(X)=\frac{1}{n}\sum _{i=1}^n(x_i^2-2\cdot \mu \cdot x_i+{\mu }^2)=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \sum _{i=1}^n(\mu \cdot x_i)+\sum _{i=1}^n({\mu }^2))=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \sum _{i=1}^n(\mu \cdot x_i)+n\cdot ({\mu }^2))$

$=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \mu \cdot \sum _{i=1}^n(x_i)+n\cdot ({\mu }^2))=\frac{1}{n}(S_2-2\cdot S_1/n\cdot S_1+n\cdot ((S_1/n{)}^2))=\frac{1}{n}(S_2-(S_1{)}^2/n)$

burada $\mu =S_1/n$ ve $S_2=\sum _{i=1}^n(x_i^2)$'dir.

Ortalamanın tahminine benzer ($\mu$) ve varyans ($Var$), bu, sırasıyla görüntünün birinci ve ikinci gücünün integral görüntülerini gerektirir (yani $I,I^2$); görüntülerin üçüncü ve dördüncü kuvvetlerine yukarıda bahsedilenlere benzer manipülasyonlar yapılabilir (ör. $I^3(x,y),I^4(x,y)$.) çarpıklık (skewness) ve basıklığı (kurtosis) elde etmek için. Ancak, F Shafait ve diğerleri tarafından belirtildiği gibi, yukarıdaki yöntemler için akılda tutulması gereken önemli bir uygulama ayrıntısı, 32 bitlik tam sayıların kullanılması durumunda yüksek dereceli integral görüntüler için meydana gelen tam sayı taşmasıdır.

Dış bağlantılar

• Nesne algılamada özet tablo uygulaması Şablon:Webarşiv

Ders videoları

• Entegre görüntü algoritmasının arkasındaki teoriye giriş (Youtube Video) Şablon:Webarşiv
• Wolfram Demonstrations Project'ten entegre görüntü algoritmasının sürekli bir versiyonunun gösterimi (Youtube Video) Şablon:Webarşiv

İlave okumalar

• Ömer Faruk SÖYLEMEZ, (Ekim 2012), İNSAN YÜZÜ İMGELERİNDE DAİRESEL HOUGH DÖNÜŞÜMÜ KULLANILARAK GÖZ DURUMU TESPİTİ, Fırat Üniversitesi, Yüksek Lisans Tezi, s. 12
• Mehmet Emin Tenekeci, Abdülkadir Gümüşçü, Ahmet Baytak, Emrah Aslan, (2014), Görüntüden OpenCV ile Duygu Analizi, Bildiri Şablon:Webarşiv
• Gökmen, Muhittin & Bayhan, Mehmet Şerif, (Haziran 2008), Ölçekten Ve Pozdan Bağımsız Gerçek Zamanlı Yüz Bulma Ve İzleme, Yüksek Lisans Tezi