Trigonometrik yerine koyma

Şablon:Kalkülüs Matematikte, bir trigonometrik yerine koyma veya trigonometrik ikame, trigonometrik fonksiyon yerine başka bir ifadeyi koyar. Kalkülüste trigonometrik ikameler integralleri hesaplamak için kullanılan bir tekniktir. Bu durumda, radikal fonksiyon içeren bir ifade trigonometrik bir ifade ile değiştirilir. Trigonometrik özdeşlikler cevabı basitleştirmeye yardımcı olabilir. Diğer yerine koyma yoluyla integrasyon yöntemlerinde olduğu gibi, belirli bir integrali değerlendirirken, integrasyon sınırlarını uygulamadan önce, ters türevin sonucunu tam olarak çıkarmak daha basit olabilir.

Durum I: a² − x² içeren integraller

$x=a\sin \theta ,$ olsun ve $1-{\sin }^2\theta ={\cos }^2\theta$ özdeşliğini kullanın.

Durum I için örnekler

Şablon:Ortala

Örnek 1

$$\int \frac{dx}{\sqrt{a^2-x^2}},$$

integralinde,

$$x=a\sin \theta ,dx=a\cos \theta d\theta ,\theta =\arcsin \frac{x}{a}.$$

ikamesini kullanabiliriz. Böylece,

$$\begin{array}{cc}\int \frac{dx}{\sqrt{a^2-x^2}}& =\int \frac{a\cos \theta d\theta }{\sqrt{a^2-a^2{\sin }^2\theta }}\\ & =\int \frac{a\cos \theta d\theta }{\sqrt{a^2(1-{\sin }^2\theta )}}\\ & =\int \frac{a\cos \theta d\theta }{\sqrt{a^2{\cos }^2\theta }}\\ & =\int d\theta \\ & =\theta +C\\ & =\arcsin \frac{x}{a}+C.\end{array}$$

Yukarıdaki adım $a>0$ ve $\cos \theta >0$ olmasını gerektirir. $a$'yı $a^2$'nin ana kökü olarak seçebilir ve ters sinüs fonksiyonunu kullanarak $-\pi /2<\theta <\pi /2$ kısıtlamasını uygulayabiliriz.

Belirli bir integral için, integrasyon sınırlarının nasıl değiştiğini bulmak gerekir. Örneğin, $x$ $0$'dan $a/2$'ye giderken $\sin \theta$ $0$'dan $1/2$'ye gider, böylece $\theta$ $0$'dan $\pi /6$'ya gider. Öyleyse,

$$\underset{0}{\overset{a/2}{\int }}\frac{dx}{\sqrt{a^2-x^2}}=\underset{0}{\overset{\pi /6}{\int }}d\theta =\frac{\pi }{6}.$$

Sınırları seçerken biraz dikkatli olmak gerekir. Yukarıdaki integral $-\pi /2<\theta <\pi /2$ gerektirdiğinden, $\theta$ yalnızca $0$ ile $\pi /6$ arasında olabilir. Bu kısıtlama ihmal edildiğinde, $\theta$'nın $\pi$'den $5\pi /6$'ya gitmesi seçilebilirdi, bu da gerçek değerin negatifiyle sonuçlanırdı.

Alternatif olarak, sınır koşullarını uygulamadan önce belirsiz integralleri tam olarak değerlendirin. Bu durumda, ters türev daha önce olduğu gibi şu sonucu verir:

$$\underset{0}{\overset{a/2}{\int }}\frac{dx}{\sqrt{a^2-x^2}}=\arcsin \left(\frac{x}{a}\right){|}_0^{a/2}=\arcsin \left(\frac{1}{2}\right)-\arcsin (0)=\frac{\pi }{6}$$

Örnek 2

$$\int \sqrt{a^2-x^2}dx,$$

integrali, $x=a\sin \theta ,dx=a\cos \theta d\theta ,\theta =\arcsin \frac{x}{a},$ burada $a>0$ olarak alınarak hesaplanabilir, böylece $\sqrt{a^2}=a$ ve $-\pi /2\le \theta \le \pi /2$ arksin değer kümesine göre $\cos \theta \ge 0$ ve $\sqrt{{\cos }^2\theta }=\cos \theta$'dır.

Böylece, $$\begin{array}{cc}\int \sqrt{a^2-x^2}dx& =\int \sqrt{a^2-a^2{\sin }^2\theta }(a\cos \theta )d\theta \\ & =\int \sqrt{a^2(1-{\sin }^2\theta )}(a\cos \theta )d\theta \\ & =\int \sqrt{a^2({\cos }^2\theta )}(a\cos \theta )d\theta \\ & =\int (a\cos \theta )(a\cos \theta )d\theta \\ & =a^2\int {\cos }^2\theta d\theta \\ & =a^2\int \left(\frac{1+\cos 2\theta }{2}\right)d\theta \\ & =\frac{a^2}{2}(\theta +\frac{1}{2}\sin 2\theta )+C\\ & =\frac{a^2}{2}(\theta +\sin \theta \cos \theta )+C\\ & =\frac{a^2}{2}(\arcsin \frac{x}{a}+\frac{x}{a}\sqrt{1-\frac{x^2}{a^2}})+C\\ & =\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C.\end{array}$$

Belirli bir integral için, yerine koyma işlemi gerçekleştirildikten sonra sınırlar değişir ve $\theta =\arcsin \frac{x}{a}$ denklemi kullanılarak $-\pi /2\le \theta \le \pi /2$ aralığındaki değerlerle belirlenir. Alternatif olarak, sınır terimlerini doğrudan ters türev formülüne uygulayın.

Örneğin,

$$\underset{-1}{\overset{1}{\int }}\sqrt{4-x^2}dx,$$

belirli integrali, $x=2\sin \theta ,dx=2\cos \theta d\theta ,$ yerine $\theta =\arcsin \frac{x}{2}$ kullanılarak belirlenen sınırlarla hesaplanabilir.

$\arcsin (1/2)=\pi /6$ ve $\arcsin (-1/2)=-\pi /6$ olduğundan,

$$\begin{array}{cc}\underset{-1}{\overset{1}{\int }}\sqrt{4-x^2}dx& =\underset{-\pi /6}{\overset{\pi /6}{\int }}\sqrt{4-4{\sin }^2\theta }(2\cos \theta )d\theta \\ & =\underset{-\pi /6}{\overset{\pi /6}{\int }}\sqrt{4(1-{\sin }^2\theta )}(2\cos \theta )d\theta \\ & =\underset{-\pi /6}{\overset{\pi /6}{\int }}\sqrt{4({\cos }^2\theta )}(2\cos \theta )d\theta \\ & =\underset{-\pi /6}{\overset{\pi /6}{\int }}(2\cos \theta )(2\cos \theta )d\theta \\ & =4\underset{-\pi /6}{\overset{\pi /6}{\int }}{\cos }^2\theta d\theta \\ & =4\underset{-\pi /6}{\overset{\pi /6}{\int }}\left(\frac{1+\cos 2\theta }{2}\right)d\theta \\ & =2{[\theta +\frac{1}{2}\sin 2\theta ]}_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{|}_{-\pi /6}^{\pi /6}\\ & =(\frac{\pi }{3}+\sin \frac{\pi }{3})-(-\frac{\pi }{3}+\sin (-\frac{\pi }{3}))=\frac{2\pi }{3}+\sqrt{3}.\end{array}$$

Öte yandan, sınır terimlerinin daha önce elde edilen ters türev formülüne doğrudan uygulanması, daha önce olduğu gibi aşağıdaki sonucu verir:

$$\begin{array}{cc}\underset{-1}{\overset{1}{\int }}\sqrt{4-x^2}dx& ={[\frac{2^2}{2}\arcsin \frac{x}{2}+\frac{x}{2}\sqrt{2^2-x^2}]}_{-1}^1\\ & =(2\arcsin \frac{1}{2}+\frac{1}{2}\sqrt{4-1})-(2\arcsin (-\frac{1}{2})+\frac{-1}{2}\sqrt{4-1})\\ & =(2\cdot \frac{\pi }{6}+\frac{\sqrt{3}}{2})-(2\cdot (-\frac{\pi }{6})-\frac{\sqrt{3}}{2})\\ & =\frac{2\pi }{3}+\sqrt{3}\end{array}$$

Durum II: a² + x² içeren integraller

$x=a\tan \theta ,$ olsun ve $1+{\tan }^2\theta ={\sec }^2\theta$ özdeşliğini kullanın.

Durum II için örnekler

Şablon:Ortala

Örnek 1

$$\int \frac{dx}{a^2+x^2}$$

integralinde,

$$x=a\tan \theta ,dx=a{\sec }^2\theta d\theta ,\theta =\arctan \frac{x}{a},$$

yazabiliriz, böylece integral şu hale gelir:

$$\begin{array}{cc}\int \frac{dx}{a^2+x^2}& =\int \frac{a{\sec }^2\theta d\theta }{a^2+a^2{\tan }^2\theta }\\ & =\int \frac{a{\sec }^2\theta d\theta }{a^2(1+{\tan }^2\theta )}\\ & =\int \frac{a{\sec }^2\theta d\theta }{a^2{\sec }^2\theta }\\ & =\int \frac{d\theta }{a}\\ & =\frac{\theta }{a}+C\\ & =\frac{1}{a}\arctan \frac{x}{a}+C,\end{array}$$

$a\ne 0$ olmak koşuluyla.

Belirli bir integral için sınırlar, ikame işlemi gerçekleştirildikten sonra değişir ve $\theta =\arctan \frac{x}{a},$ denklemi kullanılarak $-\frac{\pi }{2}<\theta <\frac{\pi }{2}$ aralığındaki değerlerle belirlenir. Alternatif olarak, sınır terimlerini doğrudan ters türev formülüne uygulayın.

Örneğin,

$$\underset{0}{\overset{1}{\int }}\frac{4dx}{1+x^2}$$

belirli integrali, $x=\tan \theta ,dx={\sec }^2\theta d\theta ,$ yerine $\theta =\arctan x.$ kullanılarak belirlenen sınırlar ile hesaplanabilir.

$\arctan 0=0$ ve $\arctan 1=\pi /4$ olduğundan,

$$\begin{array}{cc}\underset{0}{\overset{1}{\int }}\frac{4dx}{1+x^2}& =4\underset{0}{\overset{1}{\int }}\frac{dx}{1+x^2}\\ & =4\underset{0}{\overset{\pi /4}{\int }}\frac{{\sec }^2\theta d\theta }{1+{\tan }^2\theta }\\ & =4\underset{0}{\overset{\pi /4}{\int }}\frac{{\sec }^2\theta d\theta }{{\sec }^2\theta }\\ & =4\underset{0}{\overset{\pi /4}{\int }}d\theta \\ & =(4\theta ){|}_0^{\pi /4}=4(\frac{\pi }{4}-0)=\pi .\end{array}$$

Bu arada, sınır terimlerinin ters türev formülüne doğrudan uygulanması, daha önceki gibi aşağıdaki sonucu verir:

$$\begin{array}{cc}\underset{0}{\overset{1}{\int }}\frac{4dx}{1+x^2}& =4\underset{0}{\overset{1}{\int }}\frac{dx}{1+x^2}\\ & =4{[\frac{1}{1}\arctan \frac{x}{1}]}_0^1\\ & =4(\arctan x){|}_0^1\\ & =4(\arctan 1-\arctan 0)\\ & =4(\frac{\pi }{4}-0)=\pi ,\end{array}$$

Örnek 2

$$\int \sqrt{a^2+x^2}dx$$

integrali,

$x=a\tan \theta ,dx=a{\sec }^2\theta d\theta ,\theta =\arctan \frac{x}{a}$ alınarak hesaplanabilir. Burada $a>0$ böylece $\sqrt{a^2}=a$ ve $-\frac{\pi }{2}<\theta <\frac{\pi }{2}$ arctanjant değer kümesine göre $\sec \theta >0$ ve $\sqrt{{\sec }^2\theta }=\sec \theta$'dir.

Öyleyse, $$\begin{array}{cc}\int \sqrt{a^2+x^2}dx& =\int \sqrt{a^2+a^2{\tan }^2\theta }(a{\sec }^2\theta )d\theta \\ & =\int \sqrt{a^2(1+{\tan }^2\theta )}(a{\sec }^2\theta )d\theta \\ & =\int \sqrt{a^2{\sec }^2\theta }(a{\sec }^2\theta )d\theta \\ & =\int (a\sec \theta )(a{\sec }^2\theta )d\theta \\ & =a^2\int {\sec }^3\theta d\theta .\\ \end{array}$$

Sekant kübün integrali, kısmi integral kullanılarak hesaplanabilir. Sonuç olarak,

$$\begin{array}{cc}\int \sqrt{a^2+x^2}dx& =\frac{a^2}{2}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\ & =\frac{a^2}{2}(\sqrt{1+\frac{x^2}{a^2}}\cdot \frac{x}{a}+\ln |\sqrt{1+\frac{x^2}{a^2}}+\frac{x}{a}|)+C\\ & =\frac{1}{2}(x\sqrt{a^2+x^2}+a^2\ln \left|\frac{x+\sqrt{a^2+x^2}}{a}\right|)+C.\end{array}$$

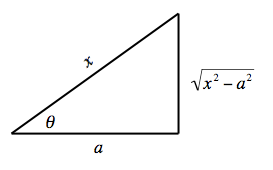
Durum III: x² − a² içeren integraller

$x=a\sec \theta ,$ olsun ve ${\sec }^2\theta -1={\tan }^2\theta .$ özdeşliğini kullanın.

Durum III için örnekler

Şablon:Ortala

$$\int \frac{dx}{x^2-a^2}$$

şeklindeki integraller, trigonometrik ikameler yerine kısmi kesirler ile de hesaplanabilir. Bununla birlikte,

$$\int \sqrt{x^2-a^2}dx$$

integrali hesaplanamaz. Bu durumda, uygun bir ikame şudur:

$$x=a\sec \theta ,dx=a\sec \theta \tan \theta d\theta ,\theta =\mathrm{arcsec}\frac{x}{a},$$

burada $a>0$ böylece $\sqrt{a^2}=a$ ve $x>0$ varsayımıyla $0\le \theta <\frac{\pi }{2}$ olur, böylece $\tan \theta \ge 0$ ve $\sqrt{{\tan }^2\theta }=\tan \theta$ olur.

Öyleyse, $$\begin{array}{cc}\int \sqrt{x^2-a^2}dx& =\int \sqrt{a^2{\sec }^2\theta -a^2}\cdot a\sec \theta \tan \theta d\theta \\ & =\int \sqrt{a^2({\sec }^2\theta -1)}\cdot a\sec \theta \tan \theta d\theta \\ & =\int \sqrt{a^2{\tan }^2\theta }\cdot a\sec \theta \tan \theta d\theta \\ & =\int a^2\sec \theta {\tan }^2\theta d\theta \\ & =a^2\int (\sec \theta )({\sec }^2\theta -1)d\theta \\ & =a^2\int ({\sec }^3\theta -\sec \theta )d\theta .\end{array}$$

Pay ve paydayı $(\sec \theta +\tan \theta )$ ile çarparak sekant fonksiyonunun integrali ve parçalarla sekant kübün integrali hesaplanabilir. Sonuç olarak,

$$\begin{array}{cc}\int \sqrt{x^2-a^2}dx& =\frac{a^2}{2}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^2\ln |\sec \theta +\tan \theta |+C\\ & =\frac{a^2}{2}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\ & =\frac{a^2}{2}(\frac{x}{a}\cdot \sqrt{\frac{x^2}{a^2}-1}-\ln |\frac{x}{a}+\sqrt{\frac{x^2}{a^2}-1}|)+C\\ & =\frac{1}{2}(x\sqrt{x^2-a^2}-a^2\ln \left|\frac{x+\sqrt{x^2-a^2}}{a}\right|)+C.\end{array}$$

$\frac{\pi }{2}<\theta \le \pi$ olduğunda ki bu da $x<0$ olduğunda olur, $\tan \theta \le 0,$ bu durumda da $\sqrt{{\tan }^2\theta }=-\tan \theta$ anlamına gelir.

Trigonometrik fonksiyonları ortadan kaldıran ikameler

Trigonometrik fonksiyonları yok etmek için ikame kullanılabilir. Örneğin,

$$\begin{array}{cccc}\int f(\sin (x),\cos (x))dx& =\int \frac{1}{\pm \sqrt{1-u^2}}f(u,\pm \sqrt{1-u^2})du& & u=\sin (x)\\ \int f(\sin (x),\cos (x))dx& =\int \frac{1}{\mp \sqrt{1-u^2}}f(\pm \sqrt{1-u^2},u)du& & u=\cos (x)\\ \int f(\sin (x),\cos (x))dx& =\int \frac{2}{1+u^2}f(\frac{2u}{1+u^2},\frac{1-u^2}{1+u^2})du& & u=\tan \left(\frac{x}{2}\right)\\ \end{array}$$

Son ikame, Weierstrass yerine koyması olarak bilinir ve tanjant yarım açı formülleri kullanır. Örneğin,

$$\begin{array}{cc}\int \frac{4\cos x}{(1+\cos x{)}^3}dx& =\int \frac{2}{1+u^2}\frac{4\left(\frac{1-u^2}{1+u^2}\right)}{{(1+\frac{1-u^2}{1+u^2})}^3}du=\int (1-u^2)(1+u^2)du\\ & =\int (1-u^4)du=u-\frac{u^5}{5}+C=\tan \frac{x}{2}-\frac{1}{5}{\tan }^5\frac{x}{2}+C.\end{array}$$

Hiperbolik yerine koyma

İntegralleri basitleştirmek için hiperbolik fonksiyonların ikameleri de kullanılabilir.

Örneğin, $1/\sqrt{a^2+x^2}$ integralini almak için, $x=a\sinh u$ (ve dolayısıyla $dx=a\cosh udu$) ikamesini, ardından ${\cosh }^2(x)-{\sinh }^2(x)=1$]] özdeşliğini kullanın:

$$\begin{array}{cc}\int \frac{dx}{\sqrt{a^2+x^2}}& =\int \frac{a\cosh udu}{\sqrt{a^2+a^2{\sinh }^{2}u}}\\ & =\int \frac{\cosh udu}{\sqrt{1+{\sinh }^{2}u}}\\ & =\int \frac{\cosh u}{\cosh u}du\\ & =u+C\\ & ={\sinh }^{-1}\frac{x}{a}+C.\end{array}$$

İstenirse, bu sonuç başka özdeşlikler kullanılarak da dönüştürülebilir, örneğin ${\sinh }^{-1}z=\mathrm{arsinh}z=\ln (z+\sqrt{z^2+1})$ bağıntısını:

$$\begin{array}{cc}{\sinh }^{-1}\frac{x}{a}+C& =\ln (\frac{x}{a}+\sqrt{\frac{x^2}{a^2}+1})+C\\ & =\ln \left(\frac{x+\sqrt{x^2+a^2}}{a}\right)+C.\end{array}$$

Ayrıca bakınız

• Yerine koyma yoluyla integrasyon
• Weierstrass yerine koyması (Weierstrass ikamesi veya Tanjant yarım açı ikamesi)
• Euler yerine koyması (Euler ikamesi)