Küme

Şablon:Dipnotsuz Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.

Tanımda geçen nesne sözcüğü aslında yeterince açıklık ifade eden bir sözcük değildir. Ama sezgisel olarak, kümeyi oluşturan nesnelerin iyice tanımlı olduklarını; yani belirgin, başka nesnelerden ayırt edilebilir şeyler olduklarını düşünüyoruz demektir. Bir bakıma, bir kümeyi oluşturan nesnelerin tek tek neler olduklarını düşünmekten çok, bir arada düşünebilir olmaları önemsenir.

Bir kümeyi oluşturan nesnelere o kümenin ögeleri veya elemanları adı verilir. Güneş, evrendeki yıldızlar kümesinin bir ögesidir. Bir kümenin ögesi olan nesne o kümenin içinde veya kümeye aittir. Küme tanımına göre bir öge ya kümenin içinde ya da içinde değildir.

İki kümenin kesişimi her iki kümede bulunan ortak ögelerden oluşur. Venn diyagramında gösterimi.

Küme Kavramının Kökeni

Georg Cantor, küme teorisinin kurucularından biri olarak, Beiträge zur Begründung der transfiniten Mengenlehre adlı eserinin başında şu tanımı vermiştir: Bir küme, algımızın veya düşüncemizin belirli, ayrık nesnelerini bir araya getirme - ki bunlara kümenin elemanları denir - işlemidir. Bu çeviride, Almancada "Menge" kelimesi "küme"(aggregate) olarak çevrilmiştir.

Küme kavramının matematiğe Georg Cantor (1845-1918) ile girdiği kabul edilir. Georg Cantor kümeyi iyi tanımlanmış ve birbirinden farklı nesneler topluluğu olarak tanımlamaktadır. İyi tanımlanmış ile kastedilen, herkes tarafından aynı şekilde anlaşılan bir tanımdır.

Cantor'dan öncede, adına küme denilmese bile matematikçiler bu kavramı yer yer örtülü bir şekilde kullanırdı. Cantor, kümeler kuramının temellerine ilişkin kapsamlı soruları ortaya koydu. Bu gelişmeler, matematiğe ve özellikle formalist akıma 20. yüzyılın ilk yarısında katkı verdi.

Almanca küme kelimesi "Menge", Bernard Bolzano tarafından Paradoxes of the Infinite adlı çalışmasında ortaya atıldı.

Küme teorisinin kurucularından Georg Cantor, transfinit küme teorisi üzerine yazdığı Beiträge zur Begründung der transfiniten Mengenlehre adlı çalışmasının başında şu tanımı verdi: Şablon:Blockquote

Bertrand Russell, küme ve sınıf arasındaki ayrımı (bir küme bir sınıftır, ancak tüm kümelerin sınıfı gibi bazı sınıflar küme değildir; bkz. Russell paradoksu) tanıttı:Şablon:Blockquote

Sezgisel kümeler kuramı

Bir kümenin en önemli özelliği, elemanlara sahip olabilmesidir; bu elemanlar aynı zamanda üyeler olarak da adlandırılır. İki küme, aynı elemanlara sahip olduklarında eşittir. Daha kesin bir ifadeyle, A ve B kümeleri, A'nın her elemanı B'nin bir elemanıysa ve B'nin her elemanı da A'nın bir elemanıysa eşittir; bu özellik kümelerin genişletilebilirliği olarak adlandırılır.Şablon:Sfn

Basit bir küme kavramı matematikte son derece faydalı olmuştur, ancak setlerin nasıl oluşturulabileceği konusunda herhangi bir kısıtlama olmadığında paradokslar ortaya çıkar:

• Russell paradoksu, "kendilerini içermeyen tüm kümelerin kümesi"nin, yani {x | x bir küme ve x ∉ x}, var olamayacağını gösterir.
• Cantor paradoksu, "tüm kümelerin kümesi"nin var olamayacağını gösterir.

Sezgisel kümeler kuramı, bir kümenin iyi tanımlanmış farklı elemanların bir koleksiyonu olarak tanımlar, ancak "iyi tanımlanmış" teriminin belirsizliği nedeniyle sorunlar ortaya çıkar.

Aksiyomatik küme kuramı

Sezgisel küme teorisinin orijinal formülasyonundan bu yana, bu paradoksları çözmek için yapılan çabalarda, setlerin(küme) özellikleri aksiyomlarla tanımlanmıştır. Aksiyomatik küme teorisi, bir küme kavramını ilkel bir kavram olarak ele alır. Aksiyomların amacı, birinci dereceden mantığı kullanarak setlerle ilgili belirli matematiksel önermelerin (ifadelerin) doğruluğunu veya yanlışlığını çıkarmak için temel bir çerçeve sağlamaktır. Ancak, Gödel'in eksiklik teoremlerine göre, birinci dereceden mantığı kullanarak herhangi bir aksiyomatik küme teorisinin paradoks içermeyen olduğunu kanıtlamak mümkün değildir.

Kümeler nasıl tanımlanır ve küme gösterimi

Matematik metinlerinde, kümeler genellikle A, B, C gibi büyük harflerle italik olarak gösterilir.Şablon:Sfn Bir küme, özellikle elemanları da set olan durumlarda, bir koleksiyon veya aile olarak da adlandırılabilir.

Sıralı gösterim

Sıralı veya numaralı gösterim, bir kümenin elemanlarını süslü parantezler arasında virgülle ayrılarak listelemek suretiyle bir küme tanımlar:

$\mathrm{A}=\{1,2,3,4\}$

$B=\{al,ak,kara,boz\}$

Bir kümede, önemli olan her elemanın içinde olup olmadığıdır, bu nedenle sıralı gösterimde elemanların sıralaması önemsizdir (buna karşılık, bir dizide, demette veya bir kümenin permütasyonunda, terimlerin sıralaması önemlidir). Örneğin, Şablon:Matematik ve Şablon:Matematikaynı kümeyi temsil eder.

Çok sayıda elemana sahip olan setler, özellikle örtük bir desene uyanlar, üyelerin listesi '...' işareti kullanılarak kısaltılabilir. Örneğin, ilk bin pozitif tam sayı kümesi, sıralı gösterimde aşağıdaki gibi belirtilebilir:

Sonsuz kümelerin sıralı gösterimi

Sonsuz bir set(küme), sonsuz bir eleman listesine sahip olan bir kümedir. Sonsuz bir seti sıralı gösterimde tanımlamak için, listeyin sonuna veya her iki ucuna da noktalama işareti konur ve bu şekilde liste sonsuz bir şekilde devam ettiği ifade edilir. Örneğin, pozitif olmayan tam sayıların kümesi aşağıdaki gibi sıralı gösterimde tanımlanabilir:

ve tüm tamsayıların kümesi ise:

Anlamsal tanım

Bir küme tanımlamanın başka bir yolu, elemanların neler olduğunu belirlemek için bir kural kullanmaktır:Şablon:Block indentŞablon:Block indent

Bu tür bir tanım, bir anlamsal açıklama olarak adlandırılır.Şablon:Sfn

Küme oluşturucu(set-builder) gösterimi

Set-builder gösterimi, elemanlar üzerindeki bir koşula dayalı olarak daha büyük bir kümeden bir seçimi belirtir. Örneğin, F kümesi aşağıdaki gibi tanımlanabilir:

Bir F kümesi, şu şekilde tanımlanabilir:

$$F=\{n\mid n\text{ bir tam sayı, ve }0\le n\le 19\}.$$

Bu gösterimde, dikey çizgi "|" "şunu ki" anlamına gelir ve tanım, "F, n'nin 0 ile 19 (dahil) arasında bir tamsayı olduğu tüm n sayılarının kümesidir" şeklinde yorumlanabilir. Bazı yazarlar dikey çizgi yerine iki nokta üst üste ":" kullanır.

Tanımlama yöntemlerinin sınıflandırılması

Felsefe, tanım türlerini sınıflandırmak için belirli terimler kullanır:

• Bir niyetsel tanım, üyeliği belirlemek için bir kural kullanır. Anlamsal tanımlar ve set-builder gösterimi kullanan tanımlar buna örnek verilebilir.
• Bir genişletici tanım, bir küme hakkında tüm elemanlarını listeleyerek tanımlar. Bu tür tanımlar aynı zamanda sayım(enumerative) niteliğindedir.
• Bir örnekleme tanımı, bir küme hakkında örnekler vererek tanımlar; noktalama işaretleri içeren bir liste bunun bir örneğidir.

Elemanı olma

Eğer B bir küme ve Şablon:Mvar B'nin bir elemanı ise, bu kısaltma şeklinde Şablon:Mvar ∈ B olarak yazılır ve aynı zamanda "Şablon:Mvar B'ye aittir" veya "Şablon:Mvar B'de bulunur" şeklinde okunabilir. Şablon:Sfn"y B'nin bir elemanı değildir" ifadesi y ∉ B şeklinde yazılır ve aynı zamanda "y B'de değil" şeklinde okunabilir.

Örneğin,$\mathrm{A}=\{1,2,3,4\}$, $B=\{mavi,beyaz,kirmizi\}$ ve $$F=\{n\mid n\text{ bir tam sayı, ve }0\le n\le 19\}.$$ kümelere göre,

4 ∈ A ve 12 ∈ F; 20 ∉ F ve yeşil∉ B.

Boş Küme

Hiçbir elemanı olmayan kümeye boş küme (veya null kümesi) denir ve hiçbir elemana sahip olmayan tek kümedir. Boş küme Şablon:Math, $\mathrm{\varnothing }$, Şablon:Math, $\{$ $\}$ veya Şablon:Mvar sembolleri ile gösterilir.

Önemli Not: $\{\mathrm{\varnothing }\}$ kümesi, boş küme ifade etmemektedir. Bu küme bir elemana sahiptir.

Birim(singleton) kümeler

Bir birim kümesi, tam olarak bir elemana sahip olan bir kümedir. Bu tür bir küme {x} şeklinde yazılabilir, burada x elemandır. {x} kümesi ve x elemanı farklı anlamlara gelir; Halmos,Şablon:Sfn bir şapka içeren bir kutunun şapkayla aynı olmadığı benzetmesini çizer.

Alt kümeler

Eğer kümenin A her elemanı aynı zamanda B kümesinde yer alıyorsa, A kümesi B'nin bir alt kümesi veya B içinde yer alan bir küme olarak tanımlanır. Bu durumu ifade etmek için A ⊆ B veya B ⊇ A şeklinde yazılır. İkinci gösterim B A'yı içerir şeklinde okunabilir. ⊆ tarafından sağlanan kümeler arası ilişkiye dahil etme veya içermeyi denir. İki küme birbirlerini içerdiklerinde eşittirler: A ⊆ B ve B ⊆ A, A = B ile eşdeğerdir.

Eğer A, B'nin bir alt kümesi ise ancak A, B'ye eşit değilse, A B'nin bir gerçek alt kümesi olarak adlandırılır. Bu durum A ⊊ B şeklinde yazılabilir. Benzer şekilde, B ⊋ A B'nin bir gerçek üst kümesi anlamına gelir, yani B A'yı içerir ve A'ya eşit değildir.

Üçüncü çift ⊂ ve ⊃ operatörleri farklı yazarlar tarafından farklı şekillerde kullanılır: bazı yazarlar A ⊂ B ve B ⊃ A ifadesini A'nın B'nin herhangi bir alt kümesini temsil etmek için kullanırken diğerleri A'nın yalnızca gerçek bir alt kümesi olduğu durumlar için A ⊂ B ve B ⊃ A kullanır.Şablon:Sfn

Örnekler:

• Tüm insanlar kümesi, tüm memeliler kümesinin uygun bir alt kümesidir.
• {1, 3} ⊂ {1, 2, 3, 4}.
• {1, 2, 3, 4} ⊆ {1, 2, 3, 4}.

Boş küme, her kümenin bir alt kümesidirŞablon:Sfn ve her küme kendisinin bir alt kümesidir:Şablon:Sfn

• ∅ ⊆ A.
• A ⊆ A.

Euler ve Venn diyagramları

A, B'nin bir alt kümesidir. B, A'nın bir üst kümesidir.

Bir Euler diyagramı, bir küme koleksiyonunun grafiksel bir temsilidir; her bir küme, içindeki elemanlarıyla birlikte bir döngü tarafından çevrili bir düzlem bölgesi olarak gösterilir. Eğer Şablon:Mvar, B'nin bir alt kümesi ise, Şablon:Mvar'yı temsil eden bölge, Şablon:Mvar'yi temsil eden bölgenin tamamen içinde yer alır. İki kümenin ortak elemanı yoksa, bölgeler birbirleriyle örtüşmez.

Buna karşılık, bir Venn diyagramı, n kümenin grafiksel bir temsilidir ve n döngü düzlemi, seçilen n kümenin her biri için (belki hepsi veya hiçbiri), seçilen kümelere ait olan ve diğerlerine ait olmayan elemanlar için bir bölge olacak şekilde düzlemi 2n bölgeye böler. Örneğin, küme Şablon:Mvar, Şablon:Mvar ve Şablon:Mvar ise, Şablon:Mvar ve Şablon:Mvar içinde bulunan ve Şablon:Mvar'nin dışında olan elemanlar için bir bölge olmalıdır (böyle elemanlar olmasa bile).

Küme Kavramları

• Eğer a elemanı A kümesine aitse bu ifade $a\in A$ olarak; ait değilse $a\in ̸A$ biçiminde göstermektedir.
• A kümesinin eleman sayısı belirtilirken s(A) veya m(A) ifadesi kullanılmaktadır.
• A ile B'nin kesişimi $A\cap B$ şeklinde gösterilmektedir.
• A ile B'nin birleşimi $A\cup B$ şeklinde gösterilmektedir.
• A'nın B'den farkı $A/B$, B'nin A'dan farkı $B/A$ olarak gösterilmektedir.
• Eğer A kümesinin elemanlarının aynısı B kümesinde de varsa $A\subseteq B$ (A,B'nin alt kümesidir.) veya $B\supseteq A$ (B, A'yı kapsar.) ifadesi kullanılmaktadır. Eğer yoksa sembollerin üstüne bir çizik atılmaktadır.
• Hiçbir ögesi bulunmayan kümeye boş küme denir. Boş küme, $\{$ $\}$ ya da $\mathrm{\varnothing }$ şeklinde gösterilmektedir. Boş küme, bütün kümelerin alt kümesidir.
• Bütün kümeleri kapsayan kümeye evrensel küme denir. Evrensel küme $\mathrm{E}$ şeklinde gösterilir.
• Eğer $s(A)\equiv s(B)$ ise A, B kümesine denktir. Eğer A ve B kümelerinin elemanları aynıysa $(A=B)$, hiçbir elemanları aynı değilse ayrık küme $(A\ne B)$ olurlar.
• $\mathrm{E}$ kümesinde A'dan ayrık olan elemanlar gösterilirken, bu elemanlar A'nın tümleyeni $(A^{\text{'}},A^{-})$ kümesinde toplanır. A'nın üstünde bir virgül veya kısa çizgi olarak gösterilir.

Kümelerin Gösterimi

Venn Şeması Örneği

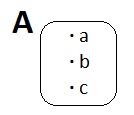
Kümenin elemanları aşağıdaki 3 yolla gösterilebilir.

• Liste Yöntemi: Kümenin elemanları $\{$ $\}$ sembolü içine, her bir elemanın arasına virgül konularak yazılır. Örneğin, $A=\{a,b,\{a,b,c\}\}$ ise, $s(A)=3$ tür.
• Ortak özellik yöntemi: Kümenin elemanlarını, daha somut ya da daha kolay algılanır biçimde gerektiğinde sözel, gerektiğinde matematiksel bir ifade olarak ortaya koyma biçimidir. $A=\{x:...\}$ Burada "$x:$" ifadesi "öyle x'lerden oluşur ki" diye okunur. Bu ifade $\{x|...\}$ biçiminde de yazılmaktadır.
• Şema Yöntemi: Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak (sol üstteki resim) gösterilir. Bu gösterime Venn şeması ile gösterimi denir.

Kullanılan Simgeler

Simge	Simgenin açıklaması	Simge	Simgenin açıklaması
∈	Elemanıdır	∪	Birleşim
∉	Elemanı değildir	∩	Kesişim
∋	Eleman olarak kapsar	⊎	Birden fazla küme bileşenleri
⊂	Alt kümesi	∅	Boş küme
⊃	Üst kümesi	≇	Ne yaklaşık ne de fiili olarak
⊆	Alt küme veya eşit	≤	Küçük veya eşit
⊇	Üst küme veya eşit	≥	Büyük veya eşit
≠	Eşit değil	≮	Küçük değil
<	Küçüktür	≰	Küçük veya eşit değil
>	Büyüktür	≱	Büyük veya eşit değil
≡	Denktir	≢	Denk değil
≈	Hemen hemen eşit	≅	Yaklaşık olarak eşit
∼	Benzer	⋚	Küçük eşit veya büyük
≫	Çok daha büyük	≪	Çok daha küçük
=	Eşit	≠	Eşit değil

Eşit Küme ve Denk Küme

Aynı elemanlardan oluşan kümelere eşit kümeler denir. Eleman sayıları eşit olan kümelere denk kümeler denir.

• A kümesi B kümesine eşit ise $A=B$ biçiminde gösterilir.
• C kümesi D kümesine denk ise $C\equiv D$ biçiminde gösterilir.

Önemli Not: Eşit olan kümeler aynı zamanda denktir. Fakat denk kümeler eşit olmayabilir.

Özel Sayı Kümeleri

Doğal sayılar N, tam sayılar Z içinde yer alır, tam sayılar Q (rasyonel sayılar) içinde yer alır, rasyonel sayılar R (gerçel sayılar) içinde yer alır ve gerçel sayılar C (kompleks sayılar) içinde yer alır.

Matematikçilerin o kadar sık atıfta bulundukları matematiksel öneme sahip kümeler vardır ki, onları tanımlamak için özel isimler ve notasyon kuralları edinmişlerdir. Bu önemli kümeler, matematik metinlerinde kalın (örneğin $𝐙$) veya tahta kalın ($\mathbb{Z}$) yazı karakteriyle temsil edilir. Bunlar şunları içerir:

• $\mathrm{N}$ veya $\mathbb{N}$, doğal sayılar kümesi: $\mathrm{N}=\{0,1,2,3,4,...\}$ (bazı matematikçiler 0'ı dahil etmemektedir.)
• $\mathrm{Z}$ veya $\mathbb{Z}$, tam sayılar kümesi (negatif tam sayılar, pozitif tam sayılar ve 0 dahil): $\mathrm{Z}=\{...,-3,-2,-1,0,1,2,3,...\}$
• $Q$ veya $\mathbb{Q}$, rasyonel sayılar kümesi (tam sayılar ve kesirli ifadeler dahil): $Q=\{a\mathrm{\setminus }b:a,b\in Z,b\ne 0\}$. Örneğin, $-3\mathrm{\setminus }2\in Q$ ve $4=4\mathrm{\setminus }1\in Q$
• $R$ veya $ℝ$, reel sayılar kümesi: [rasyonel sayılar kümesi ve irrasyonel sayılar kümesi ($\sqrt{2}$ gibi kesirli ifade biçiminde yazılamayan cebirsel sayıların yanı sıra $\pi$ ve $e$ gibi sayılar) dahil]
• $C$ veya $ℂ$, karmaşık sayılar kümesi: $C=\{a+bi:a,b\in R\}$. Örneğin, $1+2i\in C$.

Yukarıda yer alan sayı kümelerinin her biri sonsuz sayıda elemana sahiptir. Her biri bulunduğu satırın altında yer alan kümelerin bir alt kümesidir.

Pozitif veya negatif sayı kümeleri, küme sembolünün üzerine $+$ veya $-$ sembolü konularak ifade edilmektedir. Örneğin; pozitif tam sayılar kümesi $Z^{+}$, negatif tam sayılar kümesi $Z^{-}$biçiminde ifade edilmektedir.

Fonksiyonlar

Bir A kümesinden B kümesine olan bir fonksiyon (veya eşleme), her bir Şablon:Mvar kümesi elemanına Şablon:Mvar kümesinden bir "çıktı" atayan bir kuraldır; daha formel olarak, bir fonksiyon, Şablon:Mvar kümesinin her elemanını tam olarak bir Şablon:Mvar kümesi elemanına bağlayan özel bir ilişkidir. Bir fonksiyon şu şekillerde adlandırılır:

• İnjektif Birebir (veya tekil) ise, Şablon:Mvar kümesinin her iki farklı elemanını farklı Şablon:Mvar elemanlarına eşler.
• Sürjektif Örten (veya üzerine) ise, her Şablon:Mvar elemanı için en az bir Şablon:Mvar elemanı ona eşlenir.
• Bijektif Bİrebir Örten (veya bir-bir karşılıklı) ise, fonksiyon hem injektif hem de sürjektif olup her Şablon:Mvar elemanı benzersiz bir Şablon:Mvar elemanıyla eşlenir ve her Şablon:Mvar elemanı da benzersiz bir Şablon:Mvar elemanıyla eşlenir, böylece eşlenmemiş elemanlar bulunmaz.

İnjektif bir fonksiyon enjeksiyon, sürjektif bir fonksiyon sürjeksiyon ve bijektif bir fonksiyon bire-bir karşılıklı veya bijeksiyon olarak adlandırılır.

Sayallık (kardinalite)

Bir kümenin cardinality (kardinalite) değeri, o kümenin eleman sayısıdır. Örneğin, B = {mavi, beyaz, kırmızı} kümesi için |B| = 3'dür. Kümelendirmede tekrar eden elemanlar sayılmaz, bu nedenle B = {mavi, beyaz, kırmızı, mavi, beyaz} kümesi için de |B| = 3'tür.

Daha kesin bir ifadeyle, iki küme aynı kardinaliteye sahipse, aralarında bire-bir'e ilişkilendirme sağlayan bir fonksiyon bulunur.

Boş kümenin kardinalite değeri sıfırdır.

Sonsuz kümeler ve sonsuz kardinalite

Bazı kümelerin elemanları sayılamazdır veya sonsuzdur. Örneğin, doğal sayıların kümesi N sonsuzdur. Aslında, yukarıdaki bölümde bahsedilen tüm özel sayı kümeleri sonsuzdur. Sonsuz kümelerin kardinalite değeri sonsuzdur.

Bazı sonsuz kardinaliteler diğerlerinden daha büyüktür. Küme teorisi açısından en önemli sonuçlardan biri, gerçel sayıların kümesinin doğal sayıların kümesinden daha büyük kardinaliteye sahip olmasıdır. N'ye eşit veya daha küçük kardinalite değerine sahip kümeler "sayılabilir kümeler" olarak adlandırılır. Bunlar ya sonlu kümelerdir ya da N ile aynı kardinaliteye sahip "sayılabilir sonsuz kümelerdir". Bazı yazarlar "sayılabilir" terimini "sayılabilir sonsuz" anlamında kullanır. N'den daha büyük kardinalite değerine sahip kümeler "sayılabilir olmayan kümeler" olarak adlandırılır.

Ancak, bir doğru üzerindeki noktaların kardinalite değeri (yani bir doğru üzerindeki nokta sayısı), o doğrunun bir segmentinin, tüm düzlemin ve hatta herhangi bir sonlu boyutlu Öklidyen uzayın kardinalite değeriyle aynıdır.

Süreklilik hipotezi

Georg Cantor tarafından 1878 yılında formüle edilen süreklilik hipotezi, doğal sayıların kardinalite değeriyle bir doğruyun kardinalite değeri arasında bir kümenin olmadığını ifade eder. 1963 yılında Paul Cohen, süreklilik hipotezinin, Zermelo-Fraenkel küme teorisiyle (seçim aksiyomunu içeren) ZFC aksiyom sistemi içinde bağımsız olduğunu kanıtlamıştır.(ZFC, aksiyomatik küme teorisinin en yaygın olarak incelenen versiyonudur.)

Evrensel Küme

Evrensel Küme Örneği

Üzerinde işlem yapılan, bütün kümeleri kapsayan kümeye evrensel küme denir. Evrensel küme genellikle

$E$

ile gösterilmektedir. Yabancı kaynaklarda çoğunlukla

$U$

ile gösterilmektedir.

Ayrıca Bakınız

• Öge
• Gönderme (Fonksiyon)
• Bağıntı
• Kümeler kuramı
• Belirtisiz (Bulanık) Küme

Kaynakça

• Şablon:Kitap kaynağı